In this post, I want to explain why diversifying investments in a portfolio is a good idea. You might have heard that "diversification is the only free lunch in investing", but why is that the case? To explain that, I need to give you a very short introduction into Modern Portfolio Theory. It is a mathematical topic, it involves statistics, but I will make sure that everybody with an attention span to reach the end of the article should grasp the fundamental reason of why diversity helps. No equations involved.

Diversification is the only free lunch in investing.
– Nobel Prize laureate Harry Markowitz

What is volatility, and why don't we like it?

Take the following three examples. Each of these examples has the same growth-rate of 7% per year, but they have a different volatility.

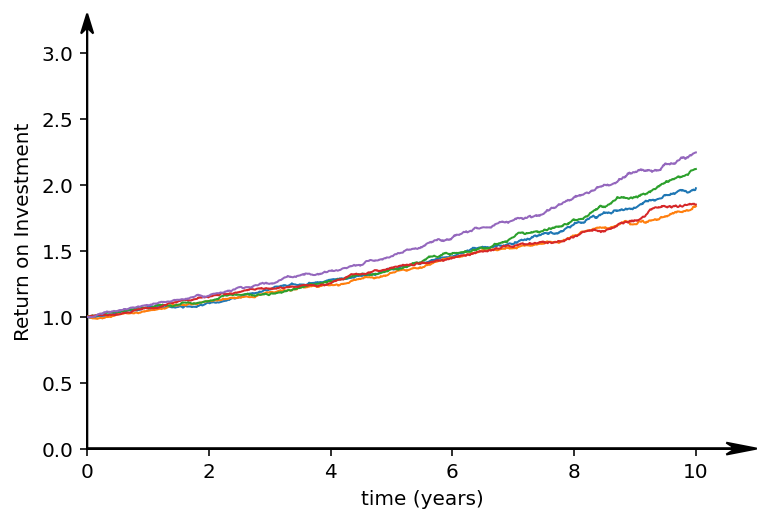
The first asset we could invest in, has an expected return on investment of 7% per year, with a volatility of 2%. Shown above are 5 different possible futures for the next 10 years. In some cases we double our investment, in some cases we gain 50%. The volatility is considerably smaller than the return on investment, so the underlying exponential curve is clearly visible.

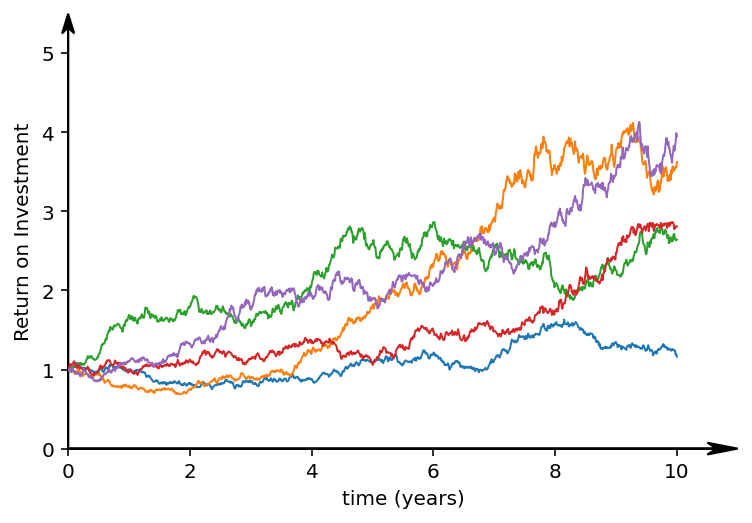
The second asset we could invest in, has an expected return on investment of 7% per year, with a volatility of 15%. This matches the volatility and growth of the S&P500. Shown here are 5 different possible futures for the next 10 years. In one case, we made a small loss. In some of the other cases, we would four-fold our original investment.

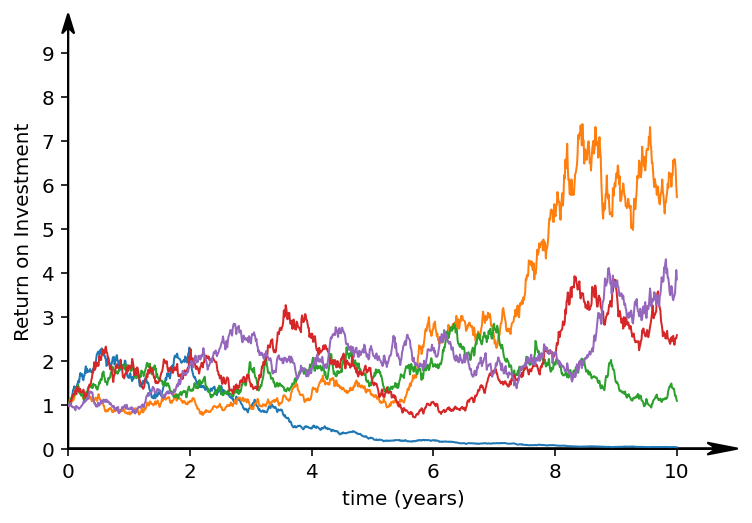
The third thing we could invest in has an expected return on investment of 7% per year, with a volatility of 38%. This volatility is akin to the volatility of Bitcoin. As you can see, in these 5 cases, one case breaks even, one goes to nearly zero after a crash in year 4, one does as well as the low volatility case and one grows a sixfold after a spurt in year 8. As you can see in this illustrative example, the growth is now completely dominated by the volatility.

There is a strict mathematical definition for this 'volatility' I am using here, namely the standard deviation of the logarithmic return on investment over one year. But, no worries if this definition is not clear, it is irrelevant for the story.

What is important to grasp, is that volatility is a measure of how uncertain you are of your returns. When volatility is low, you will typically get a growth which is close to your expected growth. When volatility is large, you will get almost random results. If it is too large, the probability of making a profit becomes fifty-fifty. At that point, you might as well start betting on coin flips rather than investing.

Therefore, Harry Markowitz argued that you want to limit the volatility of your investments. The thing you want is a guaranteed growth of your portfolio, not just an expected growth in some average case. After all, your future might not be an average one.

Now, how do you lower volatility?

Let's take a look at a simple example. Instead of thinking of stochastic processes like stocks, let us look at a much simpler stochastic problem. Imagine I have a six sided die and I have an imaginary asset whose return on investment is the number of eyes I throw in percents.

What is the return of such a dice-stock? Well, my expected return on investment is 3.5%. You can trust me that the volatility here is about 1.7%. If my portfolio only invests in this stock, the return and volatility on my portfolio will be exactly 3.5% and 1.7% as well.

Now, what happens if I diversify my portfolio over more of these dice-stocks? So instead of investing my whole portfolio into this one dice-stock, I invest half of it into a red die stock, and half of it into a blue die stock.

Well, my expected return on investment is still 3.5%. But this time, the volatility is only 1.2%! How can we see this on a more intuitive level?

Well, take a look at all possible returns my single-die-portfolio has, and how likely it is to get each of these returns:

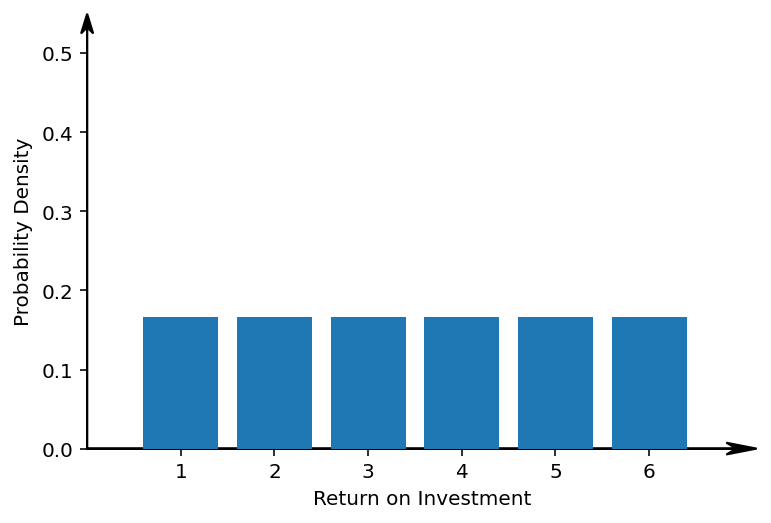
This kind of probability distribution should not be too unexpected when you throw a single die. Now, let us see what happens when we roll two dice, and look at the average number of eyes:

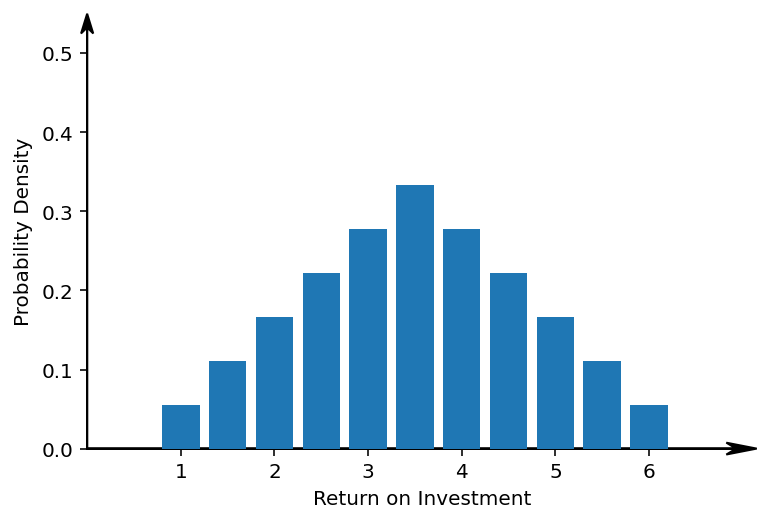
The reason for this distribution is that there are more ways to throw a 7 with two dice (1+6, 2+5, 3+4, 4+3, 5+2, 6+1) then there are to throw a 2 (only 1+1) or a 12 (only 6+6). Therefore, if you look at the average eyes of both dice, you have more ways to get a 3.5% return than a 1% or 6% return.

So apparently, when you diversify your portfolio over two separate dice-stocks, your expected return on investment is still the same, but you are more likely to get that expected return. Or in other words, you return stayed the same, but your volatility became lower!

Hey, I'm a pessimist. What is the worst case scenario here?

Let us look at the best case scenario. What if the blue die would always do the exact opposite of the red die? Mind you, it is still a blue die, with an expected return of 3.5% and a volatility of 1.7%, but it just magically happens to always do the opposite of the red die. So if red throws 1, blue throws 6. If red throws 5, blue throws 2. Let's visualise the returns of a two-dice portfolio with this magic blue die.

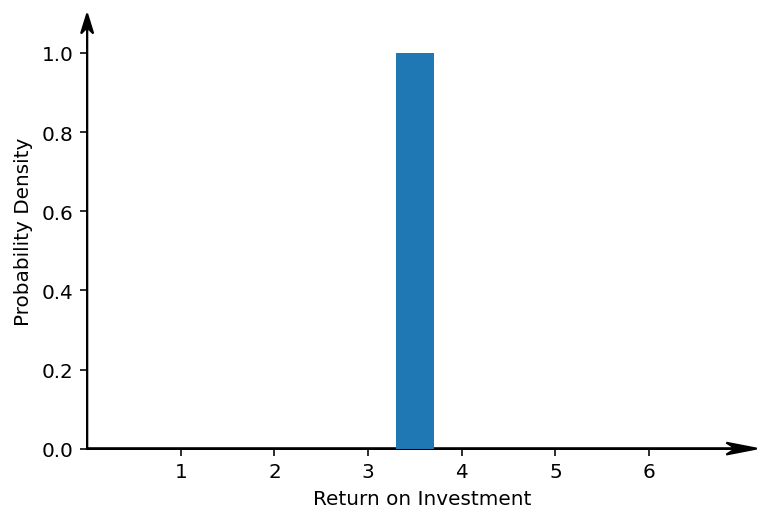
Wow, so if the blue die does the opposite of the red die, you always get exactly your expected return! There is zero volatility here. Not surprisingly, as the sum of the red and blue die will always be 7. Here, you are guaranteed to get exactly your expected return.

This magic blue die is however the best case scenario. Let's imagine the worst case scenario: the blue die magically always throws the same as the red die. Still, both dice have a return of 3.5%, both dice have a volatility of 1.7%. Let's have a look at the behaviour of our portfolio.

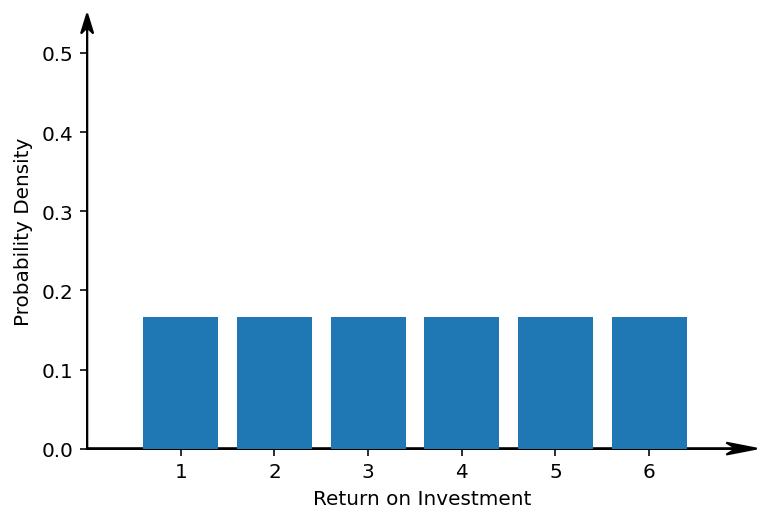
Well, that looks exactly the same as our original portfolio, where we were only investing in the red die. An expected return of 3.5%, but a volatility of 1.7%. Why is this? Well, if both dice always throw the same number of eyes, and you average their number of eyes, you might as well throw a single die and look at the eyes of that die. Nothing has changed.

What does this have to do with my stock portfolio

While the above dice-based stocks might be artificial, what they say about portfolios is true in general! If you have multiple funds with similar return and volatility:

• If you diversify over similar stocks, your return stays the same, but the volatility goes down!
• In the absolute best case of this diversified approach, you can keep your returns while removing all volatility.
• In the absolute worst case, you cannot do worse than having picked a single fund. So diversifying can only improve your portfolio, it cannot make it worse.

And that is why diversification is coined "a free lunch". You can only lower your volatility, and it does not come at a cost in returns. And as we have shown with the examples at the beginning of the article, low volatility is a desirable property as it makes returns more reliable.

However, based on the above, this free lunch does come with some caveats:

• First, volatility and returns from the past will not necessarily stay the same in the future. In this post, we kind of assumed that we knew the volatility and the expected return of our assets in the future, which we don't really, of course.
• Second, the above works for similar investments. But when stocks are dissimilar, the above explanation becomes a bit more complex. Modern Portfolio Theory is essentially the exact approach to the problem of dissimilar assets.

And that's it! If you have questions, feel free to leave a comment below, no account needed. There is no algorithm that needs nudging to send more people this way, but I can update this post based on your comments for future readers.